On This Page:
A z-score describes the position of a raw score in terms of its distance from the mean when measured in standard deviation units. The z-score is positive if the value lies above the mean and negative if it lies below the mean.
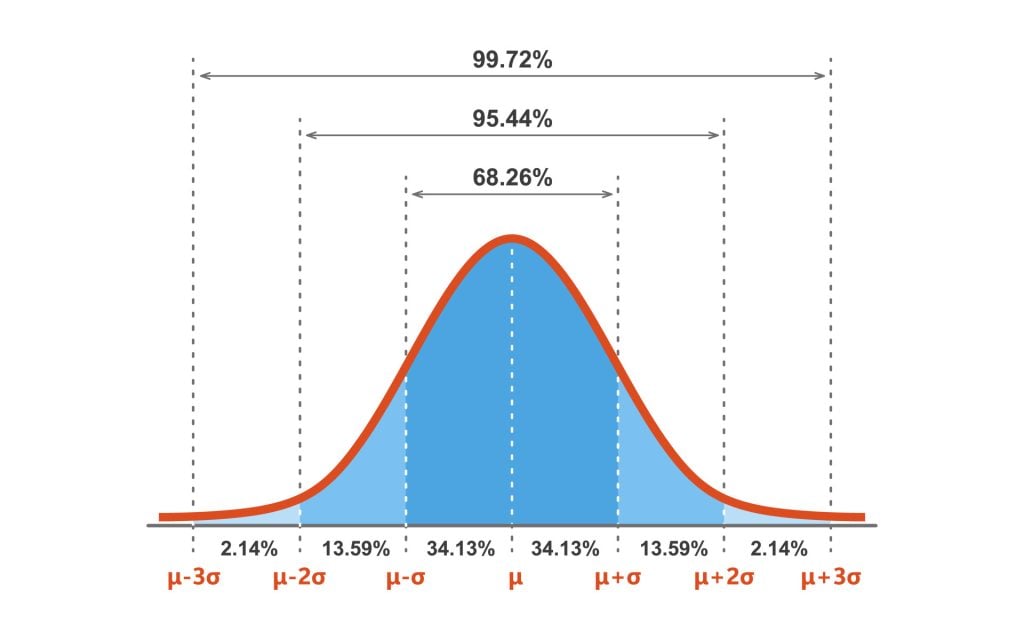
It is also known as a standard score because it allows the comparison of scores on different kinds of variables by standardizing the distribution. A standard normal distribution (SND) is a normally shaped distribution with a mean of 0 and a standard deviation (SD) of 1 (see Fig. 1).
Why Are Z-Scores Important?
It is useful to standardize the values (raw scores) of a normal distribution by converting them into z-scores because:
- It allows researchers to calculate the probability of a score occurring within a standard normal distribution;
- It enables us to compare two scores from different samples (which may have different means and standard deviations).
How To Calculate
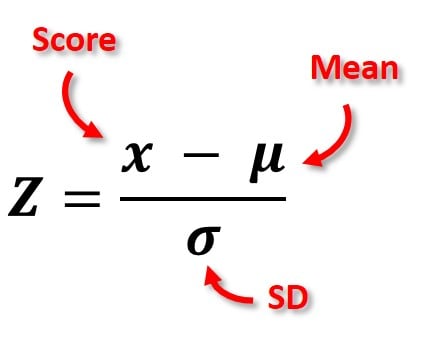
The formula for calculating a z-score is z = (x-μ)/σ, where x is the raw score, μ is the population mean, and σ is the population standard deviation.
As the formula shows, the z-score is simply the raw score minus the population mean, divided by the population standard deviation.
When the population mean and the population standard deviation are unknown, the standard score may be calculated using the sample mean (x̄) and sample standard deviation (s) as estimates of the population values.
Interpretation
The value of the z-score tells you how many standard deviations you are away from the mean. If a z-score is equal to 0, it is on the mean.
- A positive z-score indicates the raw score is higher than the mean average. For example, if a z-score is equal to +1, it is 1 standard deviation above the mean.
- A negative z-score reveals the raw score is below the mean average. For example, if a z-score is equal to -2, it is two standard deviations below the mean.
Another way to interpret z-scores is by creating a standard normal distribution, also known as the z-score distribution, or probability distribution (see Fig. 3).
Standard Normal Distribution (SND)
- The SND (i.e., z-distribution) is always the same shape as the raw score distribution. For example, if the distribution of raw scores is normally distributed, so is the distribution of z-scores.
- The mean of any SND always = 0.
- The standard deviation of any SND always = 1. Therefore, one standard deviation of the raw score (whatever raw value this is) converts into 1 z-score unit.
The SND allows researchers to calculate the probability of randomly obtaining a score from the distribution (i.e., sample). For example, there is a 68% probability of randomly selecting a score between -1 and +1 standard deviations from the mean (see Fig. 3).
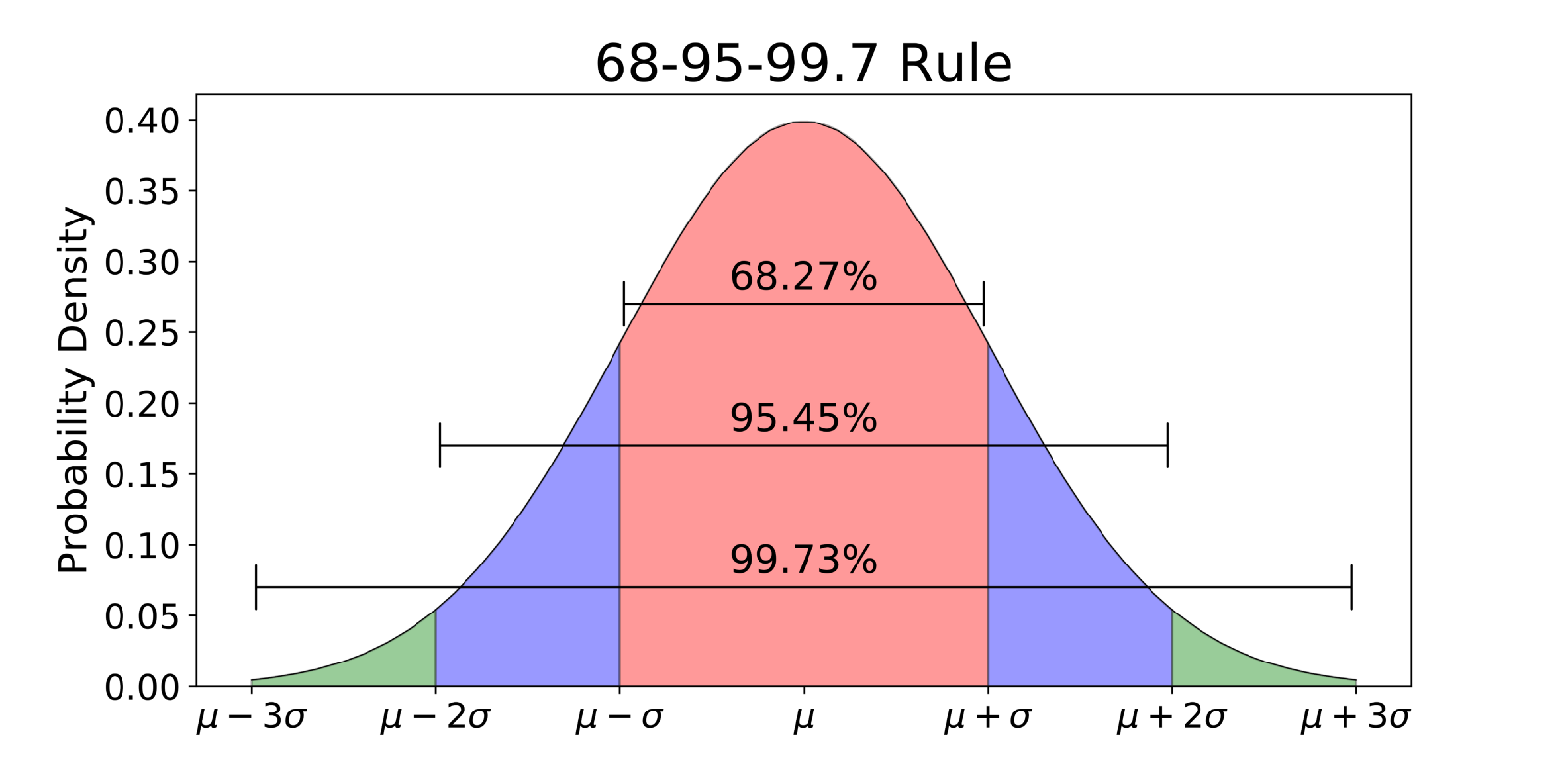
The probability of randomly selecting a score between -1.96 and +1.96 standard deviations from the mean is 95% (see Fig. 3).
If there is less than a 5% chance of a raw score being selected randomly, then this is a statistically significant result.
Learn how to use a z-score table
Practice Problems for Z-Scores
Calculate the z-scores for the following:
Sample Questions
- Scores on a psychological well-being scale range from 1 to 10, with an average score of 6 and a standard deviation of 2. What is the z-score for a person who scored 4?
- On a measure of anxiety, a group of participants show a mean score of 35 with a standard deviation of 5. What is the z-score corresponding to a score of 30?
- A depression inventory has an average score of 50 with a standard deviation of 10. What is the z-score corresponding to a score of 70?
- In a study on sleep, participants report an average of 7 hours of sleep per night, with a standard deviation of 1 hour. What is the z-score for a person reporting 5 hours of sleep?
- On a memory test, the average score is 100, with a standard deviation of 15. What is the z-score corresponding to a score of 85?
- A happiness scale has an average score of 75 with a standard deviation of 10. What is the z-score corresponding to a score of 95?
- An intelligence test has a mean score of 100 with a standard deviation of 15. What is the z-score that corresponds to a score of 130?
Answers for Sample Questions
Double-check your answers with these solutions. Remember, for each problem, you subtract the average from your value, then divide by how much values typically vary (the standard deviation).
- Z-score = (4 – 6)/2 = -1
- Z-score = (30 – 35)/5 = -1
- Z-score = (70 – 50)/10 = 2
- Z-score = (5 – 7)/1 = -2
- Z-score = (85 – 100)/15 = -1
- Z-score = (95 – 75)/10 = 2
- Z-score = (130 – 100)/15 = 2
Calculating a Raw Score
Sometimes we know a z-score and want to find the corresponding raw score. The formula for calculating a z-score in a sample into a raw score is given below:
X = (z)(SD) + mean
As the formula shows, the z-score and standard deviation are multiplied together, and this figure is added to the mean.
Check your answer makes sense: If we have a negative z-score, the corresponding raw score should be less than the mean, and a positive z-score must correspond to a raw score higher than the mean.
Calculating a Z-Score using Excel
To calculate the z-score of a specific value, x, first, you must calculate the mean of the sample by using the AVERAGE formula.
For example, if the range of scores in your sample begins at cell A1 and ends at cell A20, the formula =AVERAGE(A1:A20) returns the average of those numbers.
Next, you must calculate the standard deviation of the sample by using the STDEV.S formula. For example, if the range of scores in your sample begins at cell A1 and ends at cell A20, the formula = STDEV.S (A1:A20) returns the standard deviation of those numbers.
Now to calculate the z-score, type the following formula in an empty cell: = (x – mean) / [standard deviation].
To make things easier, instead of writing the mean and SD values in the formula, you could use the cell values corresponding to these values. For example, = (A12 – B1) / [C1].
Then, to calculate the probability for a SMALLER z-score, which is the probability of observing a value less than x (the area under the curve to the LEFT of x), type the following into a blank cell: = NORMSDIST( and input the z-score you calculated).
To find the probability of LARGER z-score, which is the probability of observing a value greater than x (the area under the curve to the RIGHT of x), type: =1 – NORMSDIST (and input the z-score you calculated).
Frequently Asked Questions
Can z-scores be used with any type of data, regardless of distribution?
Z-scores are commonly used to standardize and compare data across different distributions. They are most appropriate for data that follows a roughly symmetric and bell-shaped distribution.
However, they can still provide useful insights for other types of data, as long as certain assumptions are met. Yet, for highly skewed or non-normal distributions, alternative methods may be more appropriate.
It’s important to consider the characteristics of the data and the goals of the analysis when determining whether z-scores are suitable or if other approaches should be considered.
How can understanding z-scores contribute to better research and statistical analysis in psychology?
Understanding z-scores enhances research and statistical analysis in psychology. Z-scores standardize data for meaningful comparisons, identify outliers, and assess likelihood.
They aid in interpreting practical significance, applying statistical tests, and making accurate conclusions. Z-scores provide a common metric, facilitating communication of findings.
By using z-scores, researchers improve rigor, objectivity, and clarity in their work, leading to better understanding and knowledge in psychology.
Can a z-score be used to determine the likelihood of an event occurring?
No, a z-score itself cannot directly determine the likelihood of an event occurring. However, it provides information about the relative position of a data point within a distribution.
By converting data to z-scores, researchers can assess how unusual or extreme a value is compared to the rest of the distribution. This can help estimate the probability or likelihood of obtaining a particular score or more extreme values.
So, while z-scores provide insights into the relative rarity of an event, they do not directly determine the likelihood of the event occurring on their own.

